モンテカルロ法
ある問題を数値計算で解くのではなく、確率(乱数)を使用して近似解を導くモンテカルロ法というアルゴリズムがあります。
例えばモンテカルロ法を用いると、円周率を求めることができます。
まず、0~1の乱数(実数)を2つ発生させ、xとyとしてプロットします。これを何回か行うと、1×1の正方形の中に、点は均一にプロットされます。
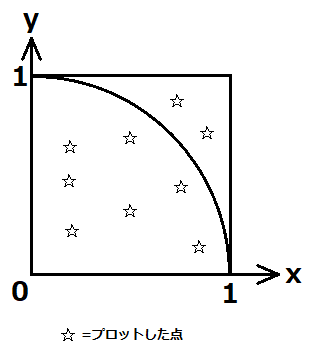
よって、正方形の面積と、1/4円の面積の比は、プロットされた点の数に比例するはずです。1/4円の中にプロットされた点の数をa、円の外にプロットされた点の数をbとすると、次の式が成り立ちます。
【計算式】
式(1)π/4:1=a:a+b
式(2)π=4a/a+b
では、実際に円周率を求めてみます。
モンテカルロ法を用いたサンプルコード(Python)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import matplotlib.pyplot as plt # 散布図用 import numpy as np # 乱数用 NUM=1000 # とりあえず点1000個でやってみる x=0 # 点のx値 y=0 # 点のy値 pai=0.0 # 求めた円周率を入れる a=0 # 1/4の円に入ってる点の数をカウント i=0 # ループカウンタ while i<NUM: # NUM回ループ x=np.random.rand() # ランダムな点の位置x y=np.random.rand() # ランダムな点の位置y if x*x+y*y<=1: # 原点との距離が1未満なら a+=1 # 1/4の円中なのでカウント plt.scatter(x,y,color='red') # 赤い点で書く else: # 円の外 plt.scatter(x,y,color='blue') # 青い点で書く i+=1 # ループカウンタ増 pai=4*a/NUM # 円周率を求める 式(2) print(pai) # 円周率確認表示 plt.show() # 散布図出力 |
【実行結果】
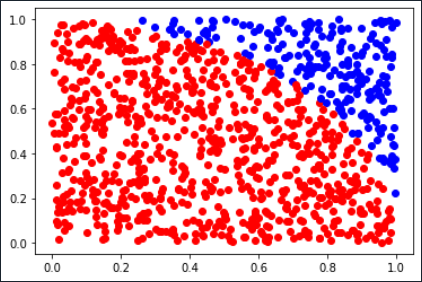
3.156
円周率は3.141…ですから、今回の実行結果はそれほど正確ではありませんが、大きく外れている訳でもありません。何度か実行すると分かりますが、点の数は同じでも計算結果は変わります。つまり、精度は、乱数がどれだけ均一にバラけたかに依存する事が分かります。
この様に、モンテカルロ法を用いると、数式を解析的に解くのが困難な場合でも近似解を求めることができます。
また、どのプログラミング言語でもモンテカルロ法で円周率を求めることはできますが、可視化が簡単なPythonで紹介しました。
さいごに
モンテカルロという名前は、ギャンブルで有名なモナコ公国のモンテカルロ地区にちなんで、乱数を用いた賭け事の様な方法であることから名付けられたそうです。(諸説あります)